Your Summe aller natuerlichen zahlen images are ready in this website. Summe aller natuerlichen zahlen are a topic that is being searched for and liked by netizens now. You can Download the Summe aller natuerlichen zahlen files here. Find and Download all free images.
If you’re searching for summe aller natuerlichen zahlen images information connected with to the summe aller natuerlichen zahlen keyword, you have pay a visit to the right blog. Our site always gives you hints for viewing the maximum quality video and picture content, please kindly surf and locate more informative video content and graphics that match your interests.
Summe Aller Natuerlichen Zahlen. Die Division durch 2 468 lässt also den Rest 1 234. Das ist kein Witz und spielt sogar in der Physik eine Rolle. Wie aber kann die Gleichung stimmen. Mist hatte Adam Riese in Erinnerung.
1 2 3 4 5 6 1 12 Mathlog From scienceblogs.de
Den beiden Forschern macht es sichtlich Spaß das absurde Ergebnis auf überzeugende Weise herzuleiten. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features. Mist hatte Adam Riese in Erinnerung. Die Summe der Zahlen von 1 bis n ist nn12 also ist die summe von x bis y die Summe von 1 bis y minus die Summe von 1 bis x-1 also yy12 - x-1x2. So lange bis sie einen allgemeine gültigen ausdruck für sn vermuten können. 1000 x 1001.
Die Summe aller natürlichen Zahlen ist unendlich groß.
Zuerst nehmen wir die summe von. Die Summe aller natürlichen Zahlen ist unendlich groß. Insgesamt kommt ihr damit auf 50 Zahlenpaare die jeweils die Summe 101 ergeben. S 1 ½1 11 ½12 1. Das tat er indem er gleich große Teilsummen aus der letzten und der ersten Zahl der zweiten und vorletzten usw bildete. Unter der Summe von 1 bis 100 versteht man das Aufsummieren Zusammenzählen der Zahlen von 1 bis 100.
Source: primakom.dzlm.de
2 1001000. Die naive Herangehensweise wäre nun einfach die Zahlen der Reihe nach aufzusummieren. Die erklären denselbigen Beweis. Eine der bemerkenswertesten Gleichungen der Wissenschaft besagt dass der Summe aller natürlichen Zahlen die Summe von 1 2 3 und so weiter bis ins Unendliche der Wert -112 zugewiesen werden. Rechner für die Summation mit dem Summenzeichen Sigma Σ.
Source: youtube.com
Wir berechnen die Summe der natürlichen Zahlen bis 1 die natürlich 1 ist nach der Formel. Für Bedingung 2 die man auch Induktionsschritt nennt nehmen wir an die Aussage gelte für beliebige n dh. Immer perfekt vorbereitet dank Lernvideos Übungen Arbeitsblättern Lehrer-Chat. Wir können sie beispielsweise anwenden um die Summe aller Zahlen von 1 bis 10 zu berechnen. 1 2 3 4 5 6.
Source: youtube.com
Ich gebe hier nur mal die einfachere Herleitung die auch unten im Video beschrieben wird. Es klingt absurd dass man unendlich viele positive Zahlen addieren kann um dann zu einem negativen und nicht unendlich großen Ergebnis zu kommen. Seiner Zeit sollte er die Zahlen von 1 bis 100 summieren. Die Formel zur Summe aller natürlichen Zahlen wurde der Geschichte nach von Gauß entwickelt. Unter der Summe von 1 bis 100 versteht man das Aufsummieren Zusammenzählen der Zahlen von 1 bis 100.
Source: de.wikibooks.org
Seiner Zeit sollte er die Zahlen von 1 bis 100 summieren. N100 sum1002 1001 50 101 5050 Das war wohl die Originalaufgabe n ungerade. Mit der Gaußschen Summenformel lässt sich die Summe aller natürlichen Zahlen bis zu einer Obergrenze n berechnen. Betrachten sie die summe. 1 2 3 4 5 6.
Source: mathelounge.de
Zuerst nehmen wir die summe von. Mist hatte Adam Riese in Erinnerung. Summe aller natürlichen Zahlen -112 - YouTube. Die Summe aller natürlicher Zahlen ist -112. Die Summe der ersten beiden natürlichen Zahlen ist 12 3 und die Summe der ersten n natürlichen Zahlen ist nn12.
Source: youtube.com
Immer perfekt vorbereitet dank Lernvideos Übungen Arbeitsblättern Lehrer-Chat. Die Summe ist eine wiederholte Addition mit einem Startwert m und einem Endwert n. Die Division durch 2 468 lässt also den Rest 1 234. Um die Summe der ungeraden Zahlen 7 bis 99 zu rechnen gehst du jetzt erst mal davon aus dass du alle ungeraden Zahlen bis 100 addieren möchtest das sind dann die ungeraden Zahlen 1 bis 99. Die Formel zur Summe aller natürlichen Zahlen wurde der Geschichte nach von Gauß entwickelt.
Source: lehrerfortbildung-bw.de
Man reduziert auf n-1 gerade und addiert n dazu N101 sum 1002 10011015151. Die Summe ist eine wiederholte Addition mit einem Startwert m und einem Endwert n. Zahlen lassen sich als Summe mit einer geraden Anzahl von Summanden g wie folgt darstellen. Um auf das Ergebnis zu kommen müsst ihr dann also nur noch 50 x 101 multiplizieren. Die erklären denselbigen Beweis.
Source: scienceblogs.de
Die Division der Summe durch die gerade Zahl g lässt als Rest die Hälfte von g also g2. Zahlen lassen sich als Summe mit einer geraden Anzahl von Summanden g wie folgt darstellen. Summe aller natürlichen Zahlen -112 - YouTube. 1 2 3 4 5 6. Man reduziert auf n-1 gerade und addiert n dazu N101 sum 1002 10011015151.
Source:
Und natürlich ist es auch absurd. Mist hatte Adam Riese in Erinnerung. Die naive Herangehensweise wäre nun einfach die Zahlen der Reihe nach aufzusummieren. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new features. Dies bezeichnet die Summe der ersten natürlichen Zahlen.
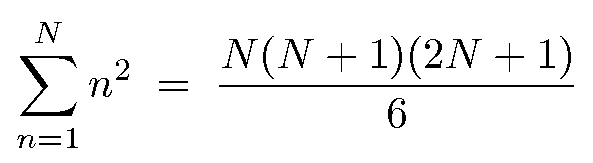Source: math.uni-bielefeld.de
Mit der Gaußschen Summenformel lässt sich die Summe aller natürlichen Zahlen bis zu einer Obergrenze n berechnen. Mist hatte Adam Riese in Erinnerung. Auf direktem Wege berechnen wir die Summe als. Mit Hilfe der Gaußschen Summenformel vereinfacht sich die Berechnung zu. Ich gebe hier nur mal die einfachere Herleitung die auch unten im Video beschrieben wird.
Source:
Die Division durch 2 468 lässt also den Rest 1 234. 2 1001000. Um die Summe der ungeraden Zahlen 7 bis 99 zu rechnen gehst du jetzt erst mal davon aus dass du alle ungeraden Zahlen bis 100 addieren möchtest das sind dann die ungeraden Zahlen 1 bis 99. Als Rechenarten sind die Grundrechenarten -. Für Bedingung 2 die man auch Induktionsschritt nennt nehmen wir an die Aussage gelte für beliebige n dh.
Source: spiegel.de
Das tat er indem er gleich große Teilsummen aus der letzten und der ersten Zahl der zweiten und vorletzten usw bildete. Nur diese Variable darf im Summenterm stehen. Es klingt absurd dass man unendlich viele positive Zahlen addieren kann um dann zu einem negativen und nicht unendlich großen Ergebnis zu kommen. Die Division durch 2 468 lässt also den Rest 1 234. S n ½n n1 und S n1 ½ n1 n11 ½ n1 n2 seien korrekt.
Source: slideplayer.org
Die Summe der ersten beiden natürlichen Zahlen ist 12 3 und die Summe der ersten n natürlichen Zahlen ist nn12. Für Bedingung 2 die man auch Induktionsschritt nennt nehmen wir an die Aussage gelte für beliebige n dh. Summe aller Quadrate bis einschließlich Summe der ungeraden Zahlen bis einschließlich Wir wollen nun eine allgemeine Form für die Summenschreibweise angeben. N100 sum1002 1001 50 101 5050 Das war wohl die Originalaufgabe n ungerade. Rechner für die Summation mit dem Summenzeichen Sigma Σ.
Source: mathelounge.de
Ich gebe hier nur mal die einfachere Herleitung die auch unten im Video beschrieben wird. Nur diese Variable darf im Summenterm stehen. 1 2 3 4 5 6 -112. Betrachten sie die summe. Die Division der Summe durch die gerade Zahl g lässt als Rest die Hälfte von g also g2.
Source: youtube.com
Es klingt absurd dass man unendlich viele positive Zahlen addieren kann um dann zu einem negativen und nicht unendlich großen Ergebnis zu kommen. Um die Summe der ungeraden Zahlen 7 bis 99 zu rechnen gehst du jetzt erst mal davon aus dass du alle ungeraden Zahlen bis 100 addieren möchtest das sind dann die ungeraden Zahlen 1 bis 99. Insgesamt kommt ihr damit auf 50 Zahlenpaare die jeweils die Summe 101 ergeben. 1 2 3 4 5 6. Die Summe aller natürlicher Zahlen ist -112.
Source: scienceblogs.de
Ad Kurze Videos erklären dir schnell einfach das ganze Thema. Das tat er indem er gleich große Teilsummen aus der letzten und der ersten Zahl der zweiten und vorletzten usw bildete. 1 2 1 1 1 displaystyle color OliveGreen1 21cdot 11. Ich gebe hier nur mal die einfachere Herleitung die auch unten im Video beschrieben wird. Als Laufvariable die bei jedem Schritt um 1 erhöht wird wird i verwendet dies muss eine ganze Zahl sein.
Source: mathelounge.de
Um auf das Ergebnis zu kommen müsst ihr dann also nur noch 50 x 101 multiplizieren. Wie aber kann die Gleichung stimmen. Es klingt vollkommen unglaublich aber es ist wahr. Aber es gilt bei geraden Zahlen. Rechner für die Summation mit dem Summenzeichen Sigma Σ.
Source: slideplayer.org
Zuerst nehmen wir die summe von. Mist hatte Adam Riese in Erinnerung. Ad Kurze Videos erklären dir schnell einfach das ganze Thema. 95 96 97 98 99 100 5050. Seiner Zeit sollte er die Zahlen von 1 bis 100 summieren.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title summe aller natuerlichen zahlen by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
